従来の統計手法と何が違う？交通事故の予測をベイズ統計を用いて検証してみた

1. はじめに
2. 前回では
3. 今回は
4. ベイズ理論とは
5. 従来の統計学との違い
- 5.1. 従来の統計学
- 5.2. ベイズ統計
6. ベイズ理論を活用した確率分布の推定
7. まとめ

はじめに

筆者は統計学を勉強中の身であり、専門家ではありません。学習時に気になったことなどを中心に、実際のデータに当てはめるとどうなるのかを目的として記載しています。

何か気になる点などがあれば教えていただけますと嬉しいです。

前回では

前回の記事では、交通事故のデータをポアソン分布を用いて表現してみるということを行いました。

よく統計学の書籍などでは交通事故や異常検知などを例としてポアソン分布が紹介されていたので、本当にそうなのか？ということを検証してみたかったためです。

交通事故の件数はポアソン分布に本当に従うのかを実際に検証してみた

交通事故は高齢者が起こすことが多い？実は40代が最も事故していて、雨よりも晴れの日に事故している

今回は

今回の記事では、確率分布の推定方法としてベイズ理論を使ってみました。ベイズ理論は、我々が持っている事前の知識と観測データを組み合わせて、確率分布を推定する方法です。

前回はシンプルなポアソン分布だけを用いて表現してみましたが、より表現力を高める手法の1つとしてベイズ統計を使うことができるとのことだったので、試してみかたったためです。

具体的には、観測されたデータを元に、ポアソン分布と呼ばれる確率分布を使ってモデルを作った後に、ベイズ統計を適用して、モデルのパラメータの事後分布を求めました。

得られた事後分布から、データがどのような確率分布に従っているのかを理解するために、ヒストグラムを作成しました。ヒストグラムは、データの値をいくつかの区間に分けて、各区間に含まれるデータの数を表したものです。

ベイズ理論とは

ベイズ理論は、確率の考え方を使って物事を理解する方法の1つです。

例えば、友達と一緒にお弁当を食べることなったとします。友達はどんなお弁当を選ぶと思いますか？

ベイズ理論では、最初に友達がどのお弁当を好むかについての予想を立てます。これを「事前確率」と呼びます。「お寿司が好きだと思う」と予想を立てた場合、他の弁当に比べて、お寿司が選ばれる確率(事前確率)は高いという予想と一緒になります。

そして、友達がお弁当を選んだ後に、その選んだお弁当の情報を知ることができます。これを「観測データ」と呼びます。たとえば、友達が実際にお寿司を選んだとしたら、それが観測データです。

ベイズ理論では、事前確率と観測データを組み合わせて「事後確率」を計算します。事後確率は、友達がお寿司を選んだ後のお弁当の確率です。これによって、観測データを考慮したお弁当の選び方を知ることができます。

ベイズ理論では、事前確率と観測データを使って確率の計算を行います。そして、その計算結果をもとに、物事をより正確に理解することができます。

例えば、友達がお寿司が好きだという事前確率が高い場合、お寿司を選ぶ確率も高いです。しかし、実際に友達がお寿司を選んだ場合、それを観測データとして考慮することで、お寿司を選ぶ確率がさらに高くなります。

ベイズ理論は、私たちが持っている情報と新しい情報を組み合わせることで、より正確な予測や判断をする手助けをしてくれるのです。

つまり、ベイズ理論は、予測や判断をするときに、最初に持っている予想と新しい情報を考慮して、より正確な答えを導き出す方法なのです。

従来の統計学との違い

従来の統計学

データの集計やパターンの分析を行い、結果を使って推測や予測をする方法です。確率の考え方は使わず、データの特徴や平均・分散などを使って分析を行います。

簡単な計算: 従来の統計は、計算が比較的簡単です。データの平均や分散などの指標を使って解析を行うことができます。
既存の手法の利用: 従来の統計には、数多くの手法やモデルがあります。これらの手法を利用することで、様々な分析を行うことができます。

ベイズ統計

確率の考え方を使ってデータの解釈や予測をする方法です。データを使って確率分布を推定し、その結果を使って推測や予測を行います。

不確かさの考慮: ベイズ統計では、推測や予測の不確かさを詳しく考えることができます。これにより、より現実的な結果を得ることができます。
事前知識の組み込み: ベイズ統計では、データだけでなく、既存の知識や経験も考慮することができます。これにより、より正確な結果を得ることができます。
柔軟性: ベイズ統計は、様々な要素や関係性を考慮に入れることができます。そのため、現実の問題に対して柔軟に対応することができます。

ベイズ理論を活用した確率分布の推定

さて、ここからが本題です。

ベイズ理論を用いたモデルでは、事前分布と事後分布を決める必要があります。

今回は交通事故のデータ

0以上の値しか取らない
上限は決まっていない
連続的ではなく離散的なデータ(体重のように小数点以下がない)

のため、事前分布はガンマ分布、事後分布としてポアソン分布を使いました。

事前分布

事前分布とは、データを収集する前に持っている知識や予想を表す確率分布のことです。具体的には、私たちがデータを見る前に、何らかの仮定や予想を立てておくことがあります。これを事前分布と呼びます。事前分布は、データに対する私たちの予想や信念を表現するものです。

事後分布とは

事後分布とは、データを考慮した後の確率分布のことです。具体的には、データを収集した後に、事前分布とデータを組み合わせて得られる新しい確率分布です。事前分布から始めて、データを考慮することで、より具体的で確かな情報を得ることができます。つまり、事後分布は、データに基づいて更新された私たちの予想や信念を表現するものです。

推定の結果(死者数のデータ)

推定の結果は下記のようにパラメータ毎(今回はラムダだけ)にどのような分布になるのかと、そのばらつきがどのようなものなのか？というアウトプットが出ます。

従来の統計では、前提として、平均や分散など「１つの真の値」があるというものでしたが、ベイズ統計の場合は「確率分布」を用いて表現するという違いがあります。

その為、事後分布として選んでいるポアソン分布ではラムダを指定してあげる必要があるのですが、このラムダも確率分布を用いて考えることになります。

$$P(X = k) = \frac{{e^{-\lambda} \cdot \lambda^k}}{{k!}}$$

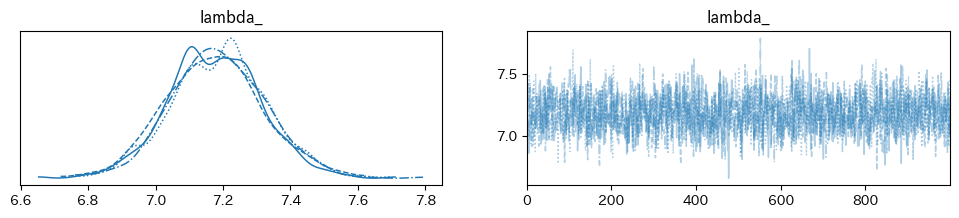
分布の収束を判断するRhatも1.1より低い値となっており、問題なさそうです。

Rhat(mean): <xarray.DataArray 'lambda_' ()>
array(1.00105469)
Rhat(median): <xarray.DataArray 'lambda_' ()>
array(1.00105469)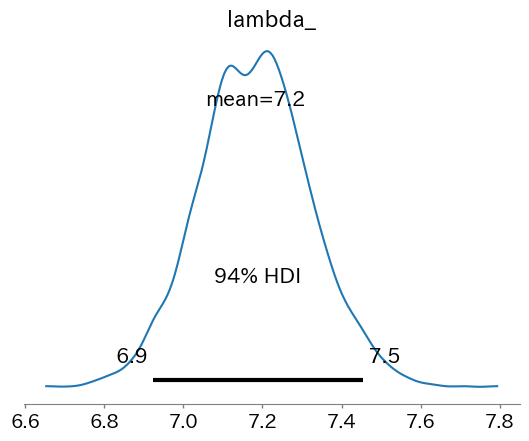

推定したラムダの平均値は7.2となりました。この結果は、前回のシンプルなポアソン分布でプロットした値と同じ結果となりました。

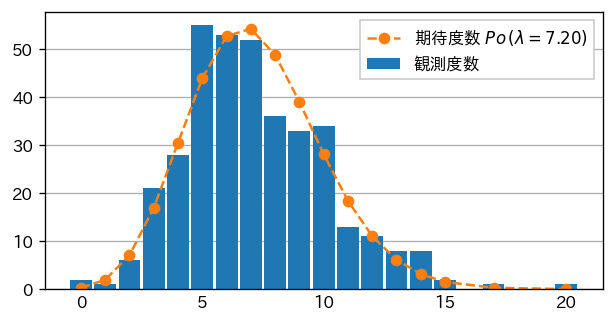
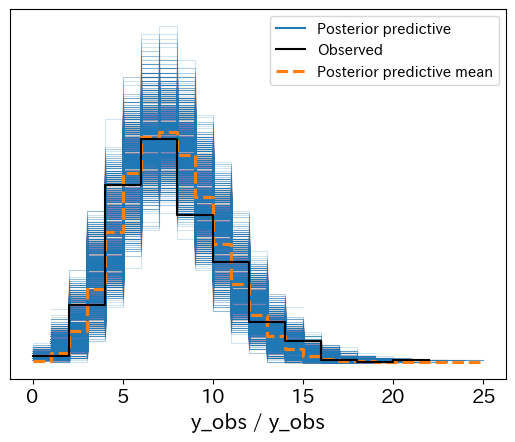
ベイズ統計を使ったポアソン分布の事後分布をサンプリングして得られたサンプル値を使ってヒストグラムを作成した結果がこちらです。

黒色が観測値のそのままのデータで、オレンジ色が推測値の平均です。

細かくみると、ブレはあるものの、大枠で見た際はおおよそ合致しているように見えます。

コード


import scipy.stats as st
import matplotlib.pyplot as plt
import scipy.optimize as opt
import pymc as pm
import arviz as az

f_num = x['死者数'].values

alpha, beta = 1.0, 1.0
# ポアソン回帰モデルのベイズ推定

with pm.Model() as model:
    lambda_ = pm.Gamma('lambda_', alpha=alpha, beta=beta)
    y_obs = pm.Poisson('y_obs', mu=lambda_, observed=f_num)

    # trace = pm.sample(1000, tune=1000, random_seed=42)
    trace = pm.sample(tune=2000, chains=4, random_seed=42)



# Rhatの計算
rhat = az.rhat(trace)
print("Rhat(mean):",rhat.lambda_.mean())
print("Rhat(median):",rhat.lambda_.median())

# Traceプロットと事後分布プロット
az.plot_trace(trace)
az.plot_posterior(trace)
plt.show()


# ヒストグラムのプロット
with model:
    pm.sample_posterior_predictive(trace, random_seed=42)
az.plot_ppc(trace)