交通事故の件数はポアソン分布に本当に従うのかを実際に検証してみた

導入

まず初めに、筆者は統計を勉強中の身で、専門家ではありません。
学習中に疑問に思ったことや気になったことを実際のデータに当てはめて、理解を深めることを目的として記載しています。

もし内容に関して何かお気づきのことがあれば、教えていただけると嬉しいです。

ポアソン分布とは

ポアソン分布は、ランダムな事象が一定の時間や場所で起こるときに使われる確率の分布です。例えば、交通事故の件数など、めったに起こらない現象を扱うときに使われます。

ポアソン分布は、平均発生数という値を使って表されます。平均発生数は、その時間や場所で平均的に何回その事象が起こるかを表しています。例えば、平均発生数が5なら、平均して5回の交通事故が起こるということです。

ポアソン分布では、その平均発生数を使って、特定の回数の事象が起こる確率を計算することができます。たとえば、平均発生数が5の場合、交通事故がちょうど3回起こる確率や、6回以上起こる確率などを計算できます。

ポアソン分布は、その特性や性質を理解するための数学的な式やグラフがあります。また、ポアソン分布を使ってデータが実際にそれに従っているかどうかを検証する統計的な手法もあります。

ポアソン分布は少し難しい概念ですが、例えば、一定の時間に平均して何回の事故が起こるかを考えるとわかりやすいかもしれません。

今回の検証の内容について

本稿では、交通事故の発生件数がポアソン分布に従うのかを検証します。具体的には、2021年の交通事故データを利用し、事故の発生件数（負傷者や死亡者の発生件数）を分析します。

警察庁Webサイトで公開されているオープンデータ(2021年)

交通事故は高齢者が起こすことが多い？実は40代が最も事故していて、雨よりも晴れの日に事故している

まずは基本統計情報を見てみる

まず初めに、交通事故の発生件数データについての基本統計情報を見てみます。

データには2021年以外のデータも含まれていたので、今回は2021年のみに絞ったデータで検証していきたいと思います。

カラム

データを見てみると、59個のカラムがありました。今回はシンプルに、死者数、負傷者数のデータのみを使ってみます。

['資料区分', '都道府県コード', '警察署等コード', '本票番号', '事故内容', '死者数', '負傷者数',
       '路線コード', '上下線', '地点コード', '市区町村コード', '発生日時\u3000\u3000年',
       '発生日時\u3000\u3000月', '発生日時\u3000\u3000日', '発生日時\u3000\u3000時',
       '発生日時\u3000\u3000分', '昼夜', '天候', '地形', '路面状態', '道路形状', '環状交差点の直径',
       '信号機', '一時停止規制\u3000標識（当事者A）', '一時停止規制\u3000表示（当事者A）',
       '一時停止規制\u3000標識（当事者B）', '一時停止規制\u3000表示（当事者B）', '車道幅員', '道路線形',
       '衝突地点', 'ゾーン規制', '中央分離帯施設等', '歩車道区分', '事故類型', '年齢（当事者A）',
       '年齢（当事者B）', '当事者種別（当事者A）', '当事者種別（当事者B）', '用途別（当事者A）', '用途別（当事者B）',
       '車両形状（当事者A）', '車両形状（当事者B）', '速度規制（指定のみ）（当事者A）', '速度規制（指定のみ）（当事者B）',
       '車両の衝突部位（当事者A）', '車両の衝突部位（当事者B）', '車両の損壊程度（当事者A）', '車両の損壊程度（当事者B）',
       'エアバッグの装備（当事者A）', 'エアバッグの装備（当事者B）', 'サイドエアバッグの装備（当事者A）',
       'サイドエアバッグの装備（当事者B）', '人身損傷程度（当事者A）', '人身損傷程度（当事者B）',
       '地点\u3000緯度（北緯）', '地点\u3000経度（東経）', '曜日(発生年月日)', '祝日(発生年月日)']

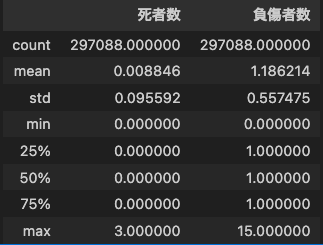
基本統計情報

データはtotalで297,088件ありました。

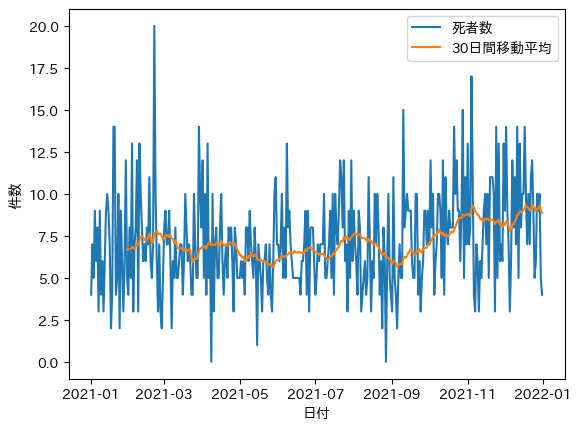
日別と移動平均(死者数)

平均で7.5前後で推移しているように見えます。

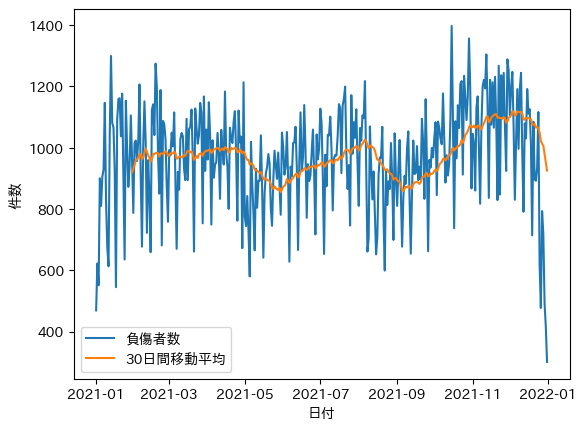
日別と移動平均(負傷者数)

平均で1000前後で推移しているように見えます。

ヒストグラム(死者数)

少し右裾が長い分布に見えます。

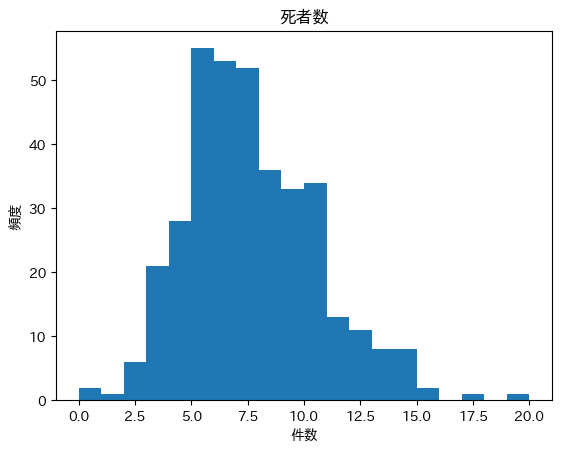
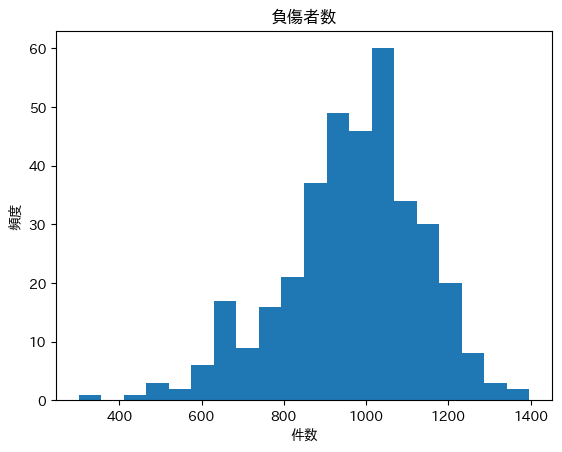
ヒストグラム(負傷者数)

左裾が長い分布に見えます。

ヒストグラムにポアソン分布を重ねてみる

次に、交通事故の発生件数のヒストグラムにポアソン分布を重ねて描画してみます。この比較を通じて、データがポアソン分布に適合しているかどうかを視覚的に評価します。

死亡者数の場合

かなり近しく分布しているように見えます。

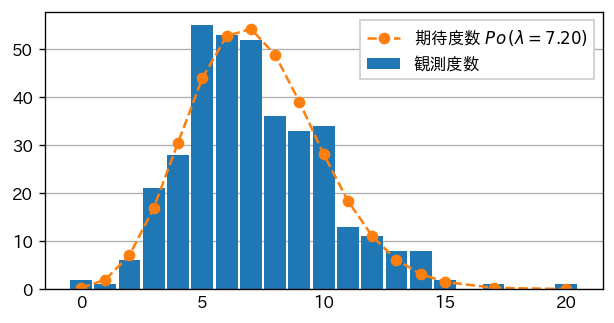
死亡者数の場合

負傷者数の場合は、binが適切に設定されていないためか、かなり見づらい感じになってしまいました。

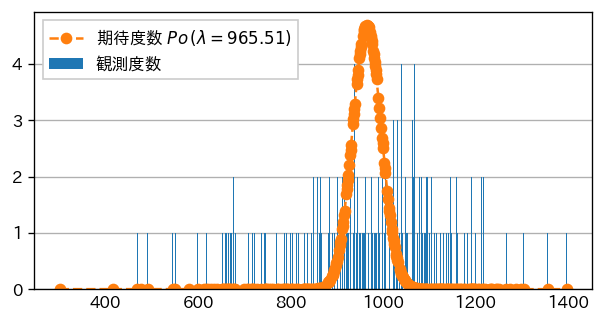
カイ2乗の適合検定をしてみる

カイ二乗検定を用いて交通事故データがポアソン分布に適合するかどうかを統計的に検証します。

負傷者の場合、ちゃんと計算ができているのか怪しいですが、一応どちらも有意水準5%で見た際に、ポアソン分布との適合があるようです。

分布をみると、1日の平均の交通事故による死者数が7.2名、負傷者数が965.5名と、普段は意識していないんですが、こんなに多いんですね。

死亡者の場合

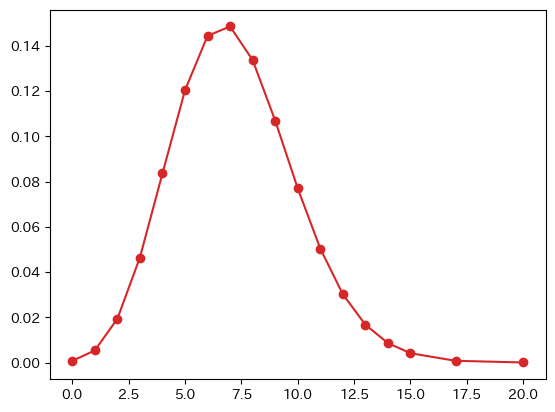
カイ二乗統計量:94.46001039825904
自由度:17 臨界値:27.58711163827534
p値:9.351408536417694e-13
有意水準5%でポアソン分布との適合あり

負傷者の場合

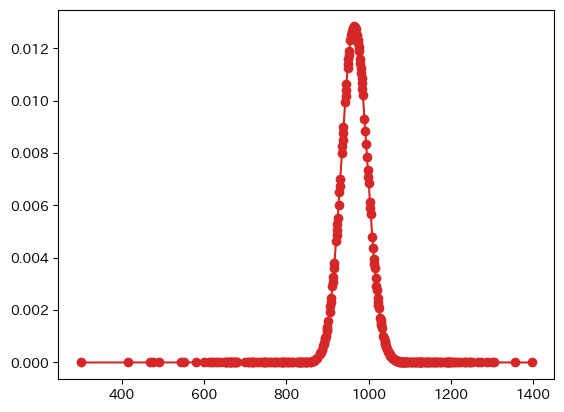
カイ二乗統計量:2.01841520222951e+135
自由度:275
臨界値:314.67836797156474
p値:0.0
有意水準5%でポアソン分布との適合あり

コード

import numpy as np
import scipy.stats as st
import japanize_matplotlib
import matplotlib.pyplot as plt

def create_data(df, column):
    df = df.groupby(column).count().reset_index()
    df = df.groupby(column, as_index=False)[['発生日時']].sum().reset_index(drop=True)
    n_cate = df[column].values
    f_num = df['発生日時'].values

    return n_cate, f_num




def poisson_test(n_cate, f_num):
    def calculate_log_likelihood(n_cate, f_num, mu_hat):
        Po = st.poisson(mu=mu_hat)  # 推定された平均クレーム数を用いてポアソン分布を作成
        pmf = Po.pmf(k=n_cate)  # k=1...7 の確率質量

        # 対数尤度を計算
        log_likelihood = np.sum(np.log(pmf) * f_num)

        return log_likelihood
    
    mu_hat = (n_cate * f_num).sum() / f_num.sum()  # 最大尤度推定による平均クレーム数の推定値
    print(f"最大尤度推定による mu_hat: {mu_hat}")
    
    log_likelihood = calculate_log_likelihood(n_cate, f_num, mu_hat)
    print(f"対数尤度: {log_likelihood}")

    Po = st.poisson(mu=mu_hat)  # 推定された平均クレーム数を用いてポアソン分布を作成
    xp = Po.pmf(k=n_cate)  # k=1...7 の確率質量
    fp = xp * f_num.sum()  # 期待度数

    plt.figure(figsize=(6, 3), dpi=120, facecolor='white')
    plt.bar(n_cate, f_num, width=0.9, label='観測度数')
    plt.plot(n_cate, fp, 'o--', c='tab:orange', label=f'期待度数 $Po\,(\\lambda={mu_hat:.2f})$')
    
    plt.tick_params(axis='x', length=0)
    plt.legend(framealpha=1, fancybox=False)
    plt.gca().set_axisbelow(True)
    plt.grid(axis='y')
    plt.show()

    expected_counts = fp

    # 観測度数の修正
    f_modified = f_num

    # カイ二乗統計量を計算
    chi2 = np.sum((f_modified - expected_counts) ** 2 / expected_counts)
    print(f'カイ二乗統計量:{chi2}')

    # 自由度を計算
    df = len(f_num) - 1
    print(f'自由度:{df}')

    # 有意水準を設定し、臨界値を計算
    alpha = 0.05
    critical_value = st.chi2.ppf(1 - alpha, df)
    print(f'臨界値:{critical_value}')

    p_value = 1 - st.chi2.cdf(chi2, df)
    print(f'p値:{p_value}')

    # 適合度を検定
    if p_value <= alpha:
        print("ポアソン分布との適合があります")
    else:
        print("ポアソン分布との適合がありません")

    plt.plot(n_cate, xp, 'o-', c='tab:red', label=f'確率質量 $Po\,(\\lambda={mu_hat:.2f})$')
    plt.show()
    
    #指定した値以下になる確率
    K = 0
    probability = Po.cdf(K)
    print(f"K以下となる確率: {probability * 100}%")

ポアソン回帰をしてみる

最後に、ポアソン回帰を用いて交通事故の発生件数を予測するモデルを構築してみます。

今回はシンプルに下記で設定してみました。

目的変数: 死亡者数
説明変数(x1): 負傷者数

定数が1.2388, x1の係数が0.0008となりました。

その日の死亡者数 = 1.2388 + その日の負傷者数 × 0.0008

と表現できそうです。

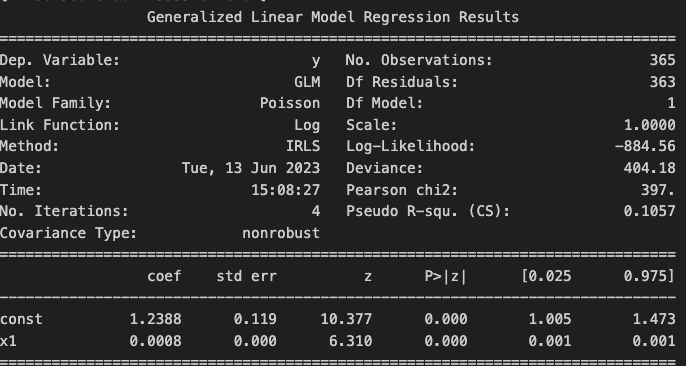
コード

#ポアソン回帰
import statsmodels.api as sm

x_lists = [['day'],['負傷者数'], ['day','負傷者数']]

for x_list in x_lists:
    # データの準備
    X = df[x_list].values  # 説明変数のデータ
    y = df['死者数'].values  # 目的変数のデータ

    # ポアソン回帰モデルの構築
    model = sm.GLM(y, X, family=sm.families.Poisson())

    # パラメータの推定
    result = model.fit()

    # 推定されたパラメータの表示
    print(result.params)

    # モデルの評価
    print(result.summary())